Pumping Water - Required Horsepower

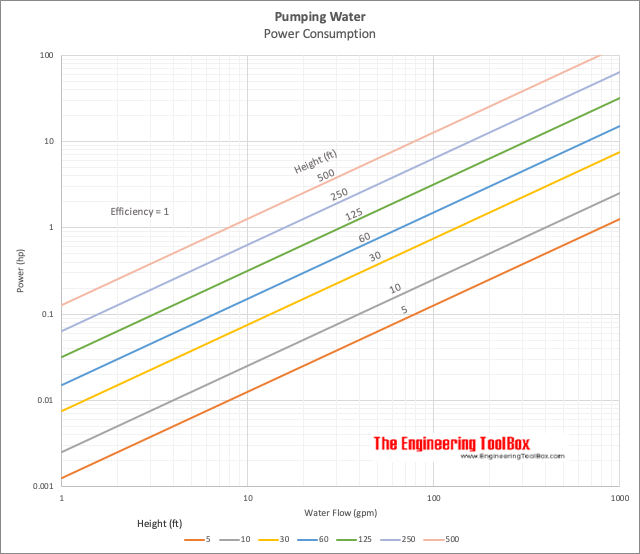
Power required to pump water at 60 o F with ideal pump efficiency 1.0:

Pumping Water - Power vs. Head and Flow
Volume Flow
(gpm)
Power (hp)
Height (ft)
51015202530354050
5 0.00631 0.0126 0.0189 0.0253 0.0316 0.0379 0.0442 0.0505 0.0631
10 0.0126 0.0253 0.0379 0.0505 0.0631 0.0758 0.0884 0.101 0.126
15 0.0189 0.0379 0.0568 0.0758 0.0947 0.114 0.133 0.152 0.189
20 0.0253 0.0505 0.0758 0.101 0.126 0.152 0.177 0.202 0.253
25 0.0316 0.0631 0.0947 0.126 0.158 0.189 0.221 0.253 0.316
30 0.0379 0.0758 0.114 0.152 0.189 0.227 0.265 0.303 0.379
35 0.0442 0.0884 0.133 0.177 0.221 0.265 0.309 0.354 0.442
40 0.0505 0.101 0.152 0.202 0.253 0.303 0.354 0.404 0.505
45 0.0568 0.114 0.170 0.227 0.284 0.341 0.398 0.455 0.568
50 0.0631 0.126 0.189 0.253 0.316 0.379 0.442 0.505 0.631
60 0.0758 0.152 0.227 0.303 0.379 0.455 0.530 0.606 0.758
70 0.0884 0.177 0.265 0.354 0.442 0.530 0.619 0.707 0.884
80 0.101 0.202 0.303 0.404 0.505 0.606 0.707 0.808 1.01
90 0.114 0.227 0.341 0.455 0.568 0.682 0.795 0.909 1.14
100 0.126 0.253 0.379 0.505 0.631 0.758 0.884 1.01 1.26

Note! Individual pump curves should always be used for exact calculations.

horsepower required to pump water to various heights

Power Consumption in Metric Units

The power consumption for pumping water can be expressed in metric units as

P = q h ρ / (6116 10 3 μ) (3)

ρ = density (kg/m 3 ) (water 1000 kg/m 3 )

μ = pump efficiency (decimal value)

Example - Power Required to Pump Water

The power required to pump 100 l/min water an elevation of 10 m (ex. friction loss in piping and efficiency = 1.0) can be calculated as

P = (100 liter/min) (10 m) (1000 kg/m 3 ) / (6116 10 3 (1.0))